[Lemma]
本文下述所使用的「小數部份」英文為 fraction (縮寫 F),此為錯誤!舊名為 Mantissa (這是我較常見到的),新名為 Significand。 - 感謝 Jacob Lee 指正。
在繼續討論之前,我假設您手邊的電腦對於有號數的負數表示法是用 2 補數表示法 (其實 "現代" 的電腦也真的是用 2 補數表示法,沒看過用 1 補數、符號大小表示法的)。
1. 電腦存取數值方式
這點只是跟大家復習一下基本的計概部份。
大家都知道電腦存數值是用二進制在存放,不是用十進制存放 (不知道的話現在知道了),用最簡單的整數而言,在 C/C++ , VB, ... etc 任何程式語言裡面,首先要知道的就是那個 "資料型態" 是用幾個 bits 去存?存下來的數值是無號數的正整數?還是有號數?
說穿了,這部份其實只是簡單的數學計算而已。
假設有 8 個 bits,每個 bit 都只能存放 0/1 ,這只是簡單的排列組合問題,一個 bit 有 2 個狀態,8個 bits 就有 2*2*2*2*2*2*2*2 = 2^8 = 256 種狀態。於是若用 8bits 表示一個 "無號數" 的話,它的範圍是 0~255,256 種狀態。然而若用 8 bits 表示一個 "有號數" 的話,我們還要考慮正負號問題,於是把它切半,256/2 = 128,範圍是 -128 ~ +127,包含 0 總共 256 個。說穿了就是下面的公式
(1.a) n bits 無號數表示範圍: 0~2^n-1
(1.b) n bits 有號數表示範圍:-2^(n-1) ~ +(2^(n-1)-1)
至於那些 int 、unsigned int 資料範圍,也是用這種方式去算出來的,不是莫名奇妙書上說 int 範圍是 -2147483648 ~ 2147483647 就是這個範圍,是因為「目前現今」的 compiler 實做 int 是給它 32 bits,算出來的表示範圍就是上面那樣。至於早期的 Turbo C (如果您還在看這類型的書,可以丟掉它了),compiler 實做 int 是給它 16 bits,所以範圍是 -32768 ~ +32767。
好了,這裡最後說明,為什麼那些做影像處理的,讀檔的時候是用 fgetc,但卻建議他們的資料型態要設成 unsigned char 而不是設 char。原因很簡單,由於 fgetc 是傳回 int,傳一次只讀 8 bits 資料,但它卻把這 8bits 解讀為 int,也就是讀出來的範圍會是 -128~+127,然而實際上 fgetc 影像取出來的值卻希望會是 00~FF,也就是 0 ~255 ,於是才建議宣告成 unsigned char。
於是別人的 library 就有自己的定義出現了,類似這種寫法
typedef char i8; // 8bits 有號數 typedef unsigned char u8; // 8bits 無號數 typedef short i16 ; // 16 bits 有號數 typedef unsigned short u16; // 16 bits 無號數 typedef int i32 ; // 32 bits 有號數 typedef unsigned int u32 ; // 32 bits 無號數 typedef long long i64; // 64 bits 有號數 typedef unsigned long long u64; // 64 bits 無號數
2. IEEE754 二進制浮點數種類
目前電腦存放浮點數都是從 IEEE754 規格,常見的有單精度(32bits 表示一個浮點數)和雙精度 (或稱倍精度,64bits 表示一個浮點數),其它延伸的有延申單精度(43bits 以上)、延伸雙精度(79 bits 以上,常以80bits 實做)。
而佔用的 bit 數愈多,代表可以表示的範圍愈大、可表示的小數點位數愈多,但相對的,佔用 bit 數愈多,計算時間 "理論上" 應會較久。注意筆者用了"理論上"三個字,原因是現代大多之 GPU,使得處理 64 bits 之浮點數比起 32 bits 之浮點數快。故若非調用顯卡 API 時 (不知道這動作沒關係,下一句才是重點),筆者建議盡量使用 64 bits 之 double ,它除了比 float 多吃 32 bits 之外,不論速度、精準度、可表示範圍都在 float 之上。
為了繼續講下去,這裡先定義出一些簡單的符號出來:
正負號:S (Signed)
指數:E (Exponent)
小數:F (Fraction)
欄位順序是 (S - E - F)
3. IEEE754 表示
這部份我只大概說一下,其它的 NAN、INFINITE 我便跳過。假設現在我定義了一份 8bits 之 浮點數表示,正負號(S)吃 1 bit,指數(E)吃 3 bits,小數(F)吃 4 bits (再次聲明,這是我假設的)。要考慮的是,即使用 IEEE754 格式存這 8 bits ,存下來的全部還是 0/1 的資料。這裡要注意的是,指數(E) 的部份在存取的時候一定會 +/- 一個 base value,以這個例子而言,我的指數(E) 是用 3 bits,它的 base value = 2^(3-1)-1 = 3。 設指數為 n bits ,base value 公式為 2^(n-1)-1。存進去時是 +base value;取出來時是 -base value。
現在,假設我將 +110.11 這個二進制浮點數存進去。步驟如下
(3.a) 決定正負號:正存 0,負存 1,而一般 C language 在 floating 表示法上,也存在著正負零之問題。
(3.b) 正規化:以二進制科學表示法進行正規化,小數點前必只有一個唯一一個1,於是轉成了1.1011 * 2^2 (小數點往左移2位,所以是 2^2),於是那個 E=2
(3.c) 調整指數:上面有提到所有指數要 +/- 一個 base value,這個例子它的 base value = 3,在存進去的時候是 + base value,取出來的時候是 - base value,於是到時候存的時候是存 2 + 3 = 5 ,二進制表示為 101
(3.d) 存進 IEEE754 欄位:存進去的時候就像這樣

至於讀出來的時候
(3.a) 讀取 +/- 號:讀到 0 ,為 +
(3.b) 讀取指數(E):讀到101,為5,再減去上 base value (=3) ,故指數部份為 2
(3.c) 讀取小數(F):讀到 1011
(3.d) 顯示完整數值:完整數值即為 +1.1011 * 2^2,也就是 110.11
問題:為何是 1.1011,而不是 0.11011 ? 答案很簡單,因 IEEE754 規定裡,在正規化時,必須正規化成小數點前一位為1,然後只存小數點後面的數字。
說明到現在,第一次接觸的人可能無法接受那個 base value,不過 IEEE754 在存 E 的時候就是要 +/- 那個 base value (好處我想是可以 "盡量" 比較精準吧 )。
base value 的算法再強調,假設有 n 個 bits 存指數,base value = 2^(n-1)-1 。
嗯,好了,接下來我們可以正式探討那些單精度、雙精度的問題了。
4. 單精度與雙精度格式
直接放一張圖上來說明單精度與雙精度格式
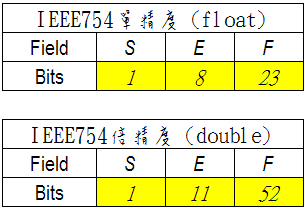
再整理一下
(4.a) 單精度浮點數:正負號 1 bit,指數部份 8 bits,小數部份 23 bits,共 32 bits
(4.b) 雙精度浮點數:正負號 1 bit,指數部份 11 bits,小數部份 52 bits,共 64 bits
這樣我們便可得到許多結論
<結論1> 精度(精確度)
單精度的小數部份是 23 bits,故 單精度浮點數之精度為2^-23 = 1.192092896 * 10^-7,這就是它的精度。
倍精度的小數部份是 52 bits,故 雙精度浮點數之精度為2^-52 = 2.220446049 * 10^-16,這就是倍精度的精度。
<結論2> 最大正數、最小負數
單精度 - 可以存的最大值是在指數裡面全都放 1,但最後一個位必需是放 0 (原因是全放 1 的已被保留作為特殊值表示用),而表示的內容還要扣掉一個 base value (2^(8-1)-1 = 127),也就是可以表示指數的最大值為 1111 1110 = 254,扣掉 base value = 254 - 127 = 127;至於小數部份全放1的數會有 32 個1;所以可以單精度可以表示的最大正數為
單精度最大正數 :+1.1111.... (小數點後23個1) * 2^127 = +(2- (2^-23)) * ( 2^127) = +3.402823668 * 10^38
雙精度最大正數 :一樣的算法, +(2-(2^-52)) * (2 ^ 1023) = +1.7976931348 * 10^308
至於最小負數,其實和上面的情況一模一樣,只是在 Signed bit 的地方從 0 改成 1 而已,於是
單精度最小負數 : -(2- (2^-32)) * ( 2^127) = -3.402823668 * 10^38
雙精度最小負數 : -(2-(2^-52)) * (2 ^ 1023) = -1.7976931348 * 10^308
相信這四個數值和各位在教科書上的 float 、dobule 可表示範圍相差無幾。
<其它結論>
至於最小正數、最大負數的問題,不是很直覺的像上面的那種算法,原因在於 IEEE 754 格式,為了能表達一些例外情況 (如無窮大、Not a number 等等),於是最小正數、最大負數並不於此處下結論 (會把文章愈拖愈長)。
這部份筆者將於 [浮點數] C/C++ 浮點數特殊值 這部份繼續探討,此篇跳過便不再深入贅述。
另需注意,並非所有 compiler 一定從 IEEE754 規格(雖然目前大多都是符合沒錯)。另即使 compiler 在一般情況下符合 IEEE754 儲存格式,但在最小正數、最大負數時會做跳一些修正,使得可表達之最小正數、最大負數比 IEEE754 規格來得小些,此部份乃屬 depends on compiler,不做深入探討。
5. 捨位誤差
由上述我們知道,不論是單精度還是雙精度,它可以表示的小數還是有限的。假設現在我把 0.8 存成單精度,由於 0.8 轉成小數會是 0.11001100110011001100... (1100 一直 loop 下去),最後存成單精度只能存那 23 bits 的小數,最後再取出來的結果可能是 0.79999998 之類的,這個就叫做捨位誤差。至於 0.2 存的話也是存成 0.001000100010001...(0001 loop 下去) 所以如果寫出這樣的程式碼是非常危險
#include <iostream> #include <cmath> int main() { float x=0.8; float y=0.2; cout << x << endl; cout << y << endl; if (fmod(x, y)==0.0) cout << "整除" << endl; return 0; }
上面這段程式碼的執行結果是看 compiler 實做,光是輸出 x 有些 compiler 就可以準到輸出 0.8,有些 compiler 卻只能輸出 0.799999 之類的數值(我只知道有些 compiler 會不準,但舉不出哪些),至於浮點數相除取餘數(fmod)的問題也會依 compiler 實做不同而有不同結果。為了避免這種情形,我們用一個簡單的方法,定義一個很小很小的數,去避開這個捨位誤差問題
#include <iostream> #include <cmath> #define EPS 1E-6 // 定義 EPS = 10^-6 int main() { float x=0.8; float y=0.2; cout << x << endl; cout << y << endl; if (fabs(fmod(x, y))<=EPS) cout << "整除" << endl; return 0; }
說到這裡關於程式設計上的 "浮點數誤差" 已經建立了相當的觀念,如果還要了解一些技巧 (比如說如何去避免大數除小數、小數除大數造成的誤差),這方面可以再去翻翻一些數值分析的書 (我沒翻過,所以版友也可以推薦)。
6. 確定 Compiler 提供之浮點數規格
最後要提醒的是,每個 Compiler 提供之浮點數規格可能不盡相同,但這些規格基本上都是在 float.h 、cfloat 裡面,我以 VC 為例,摘下一部份的內容與翻譯 (有些翻得很差,請見諒)
// 有效位數15位 #define DBL_DIG 15 // 精準度, 使 1.0 + DBL_EPSILION!=1.0 #define DBL_EPSILON 2.2204460492503131e-016 // 指數位數 #define DBL_MANT_DIG 53 // 最大值 #define DBL_MAX 1.7976931348623158e+308 // 最大十進制指數 #define DBL_MAX_10_EXP 308 // 最大二進制指數 #define DBL_MAX_EXP 1024 // 最小正整數 #define DBL_MIN 2.2250738585072014e-308 // 最小十進制指數 #define DBL_MIN_10_EXP (-307) // 最小二進制指數 #define DBL_MIN_EXP (-1021) // 指數進制基底 #define _DBL_RADIX 2 #define _DBL_ROUNDS 1 // 有效位數6位 #define FLT_DIG 6 // 精準度, 使 1.0 + FLT_EPSILION!=1.0 #define FLT_EPSILON 1.192092896e-07F #define FLT_GUARD 0 // 指數位數 #define FLT_MANT_DIG 24 // 最大值 #define FLT_MAX 3.402823466e+38F // 最大十進制指數 #define FLT_MAX_10_EXP 38 // 最大二進制指數 #define FLT_MAX_EXP 128 // 最小正整數 #define FLT_MIN 1.175494351e-38F // 最小十進制指數 #define FLT_MIN_10_EXP (-37) // 最小二進制指數 #define FLT_MIN_EXP (-125) #define FLT_NORMALIZE 0 #define FLT_RADIX 2 #define FLT_ROUNDS 1
注意到,這份定義和前面說明有幾點符合的地方,我們以 DBL (double) 為例,其他的 FLT 系列也一樣 。
(6.1) #define DBL_MANT_DIG 53
這意指 mantissa ( 也就是存浮點數的部份 ) 為 53 bits, 雖然實際上欄位是給 52 bits,但由於在正規化過程中,小數點之前的1會被藏起來,故變成了52+1 = 53。
(6.2) #define DBL_DIG 15
這部份其實只是參考而已,由於浮點數還是用二進位表示,52 個 bits 之 mantissa,精度是 2^-52,換成 10 進位約 2.2 * 10^-16,故小數點約到 15 位數左右 ( 16 位數以後沒辦法完全表達)。
(6.3) #define DBL_MAX 1.7976931348623158e+308
這個上面有推過了,雙精度最大數,也就是 +(2 - (2^-52) ) * ( 2^1024) = +1.7976931348 * 10^308,和我們上面推導的差別並不大。FLT_MAX 也是同義。
(6.4) DBL_MAX_10_EXP 與 DBL_MAX_EXP
上面定義 DBL_MAX_EPS 為 1024,是以二進位為基準,而 DBL_MAX_10_EPS 是以十進位為基準,有個關係存在 : 2^1024 = 1.80*10^308,故 DBL_MAX_10_EXP 就是 308。注意一點, DBL_MAX_EXP 之定義,並不代表必為正規化之最大指數值。DBL_MIN_10_EXP 與 DBL_MIN_EXP 也是同樣道理,只是由最大轉成最小而已。
(6.5) #define DBL_EPSILON 2.2204460492503131e-016
這個上面也有推過了,且數值相當接近 (其實是一樣的),由於 mantissa 為 52 bits,精度即為 2^(-52) = 2.2204460492503131e-016
* (6.6) DBL_MIN
這個值下面會說明,但筆者手邊之二大 compiler ( VC 系列 / gcc 系列 ) 給予的值不一樣,。這個值很重要,在一些數值分析時,若不設收斂條件時,這個值將會是拿來被參考的最小誤差,當作其收斂條件。依 IEEE754 ,正規化後之最小正數(最大負數),應為 (+/-) 2^-1022,這個值剛好等於 VC 所定義之 DBL_MIN。
問:明明有 11 bits exponment,basement = 2^(11-1)-1 = 1023,exponment 範圍應是 (0 - basement) ~ (2^11 - basement) = -1023~1025, (a) 為什麼 DBL_MIN 是 2^-1022,而不是 2^-1023? (b) 為什麼 DBL_MAX_EPS 是 1024,而不是 1025?
答: (a) 因為 2^-1023,-1023 這個值被保留下來,用來表達正負零,所以最小是 2^-1022。 (b) 因為 DBL_EPS ,1025 被保留下來分別代表正負無窮大 (也就是有時候寫 code 會看到的 #INF ),所以最大只剩 1024。
從上面分析下來的結果是:針對「正規化」之部份, VC 浮點數之處理真的完全符合 IEEE754 規格。
上述這些和我們手算的差別並不會很大 (扣除掉本篇沒提到的一些例外,[浮點數] C/C++ 浮點數特殊值 ),而上述我覺得比較有意義的應是那些 "指數位數"、"小數位數" 的定義,知道這二個之後所有東西應都推得出來。
「目前」 float: 32bits, double: 64bits, long double 在規格書上只有要求它使用的 bit 數要大於等於 double,實作上依各家 Compiler 定義,像 VC 的 long double 和 double 是一樣的東西(都是 64 bits);至於其它 Compiler 有沒有到 80 bits、128 bits,那還是去查 float.h 或 cfloat 較佳。
結束前提醒一件事,事實上定義在 float.h 裡面之 DBL_MIN / FLT_MIN,指的是「正規化」最小值,意指實際上可以經由程式語言特性上的操作,可能可以出現比 DBL_MIN / FLT_MIN 更小之值,這點於 [浮點數] C/C++ 浮點數特殊值 此篇文章將再詳述並以 C 語言實做,最後的確可顯示出比 FLT_MIN / DBL_MIN 還小之浮點數值,唯實際上在進行數學運算 (含四則運算、數學函式運算) 時,並不適合刻意去取得非正規化之最小值,如此一來運算過程將變得不準確,也不可靠。
7. 參考資料
Wiki - IEEE754
edisonx blog
MSDN - floating limits
MSDN - Integer limits



 留言列表
留言列表



 {{ article.title }}
{{ article.title }}